Fractal Math Describes How Realistic Trees Look In Art

What makes a tree a tree? Or rather, why can we recognize trees in even quite abstract depictions when they are so varied in nature? Researchers have found a clue in the branches, and used math to describe how the way we see branches in nature and art contributes to our recognition of trees.

“We’ve come up with something universal here that kind of applies to all trees in art and in nature,” Mitchell Newberry told the University of Michigan. “It’s at the core of a lot of different depictions of trees, even if they’re in different styles and different cultures or centuries.”

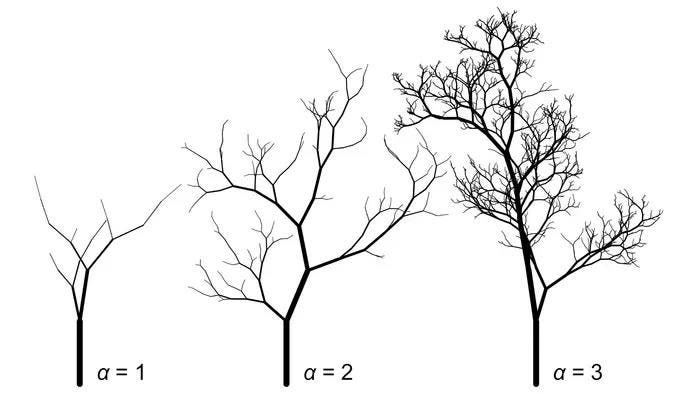
The math Newberry and his student Jingyi Gao used is based on fractals. These are patterns created by repeating the same smaller pattern within itself. Snowflakes are an example of this, but fractals can also form tree patterns. “Fractals are just figures that repeat themselves,” Gao said. “If you look at a tree, its branches are branching. Then the child branches repeat the figure of the parent branch.”

Jingyi Gao and Mitchell Newberry

Gao and Newberry used mathematical rules for fractal calculations to study these branching patterns. Part of the formula they worked with is a number referred to as the “branch diameter scaling exponent”. In real trees in nature, that number is usually somewhere between 1.5 and 3, depending on the tree. But in art, it’s all up to the artist and how they depicted their trees.

Calculating fractal branches in tree art

The study was inspired by a visit to the Sidi Saiyyed Mosque in India. Newberry noticed that some of the windows had carvings with stylized trees. Despite being a somewhat abstract representation, they were still clearly trees, and he wondered what it was that made this so obvious.

Cherry Blossoms credit to The Metropolitan Museum of Art

When Newberry and Gao calculated the branch diameter scaling exponent of the trees in the window carvings, they found that the number was closer to that of real trees than some more realistic paintings, like an 18th century painting by Matsumuara Goshun. “That was actually quite surprising for me because Goshun’s painting is more realistic,” Gao said.

To test if this value had something to do with tree recognisability in art, the researchers used two paintings by Piet Mondriaan. Known mostly for his right angles and bright colors,, Mondriaan’s older works were a bit more realistic. Over time, his style became more abstract. By 1911 he was already at the point where he only used a series of angled lines to depict a tree in “De Grijze Boom” (“The Grey Tree”). But a year later, when he painted the same tree, those lines got a bit less tree-like.

Kunstmuseum Den Haag

When Gao and Newberry calculated the branch diameter scaling exponent for the trees in both paintings, the older one was closer to the value found in nature. “The only difference between these two paintings—they’re both black strokes on a basically gray background—is whether there is branch diameter scaling,” said Newberry.

Of course, there are likely other factors that determine the realism of a tree painting. The cherry blossom painting by Goshun is clearly a (part of a) tree despite a less natural branch diameter scaling exponent. But by looking at fractals in art and trees, the researchers hoped to start a discussion. “This theory of proportion outlines an ideal, and provides common terms in which to compare art, mathematical models, and the biology of trees,” they write in their research paper. “We hope to create dialog across arts, math, and sciences to foster insights into each.”

_{Images are for reference only.Images and contents gathered automatic from google or 3rd party sources.All rights on the images and contents are with their legal original owners.}